|
Abstract
A sunlit sphere without temperature equalization will haven an average temperature of -128 °C.
Ocean, soil and atmosphere (with greenhouse gasses), the 'geotriad', make this +12 °C.
(The same sphere with full temperature equalization would average -18 °C.)
It is not well enough known which part of the temperature gap is accounted for by which triad element.
Preface
Our Earth is a pleasant planet to live on; well, may be not everywhere. It is not nice to live at the North Pole, the South Pole or in 'Death Valley', nor where you always have to tread water, or on the top of Mount Everest. But compared to the other planets, orbiting the sun, here are many places, where it is nice to be. Why on Earth and not elsewhere? There are numerous reasons for this. Too many to mention. But one of them is that Earth's temperature suits our life. That is what this lesson is about.
It is because we are neither too far from, nor too close to the sun. But that is not the whole story. For example, it does not explain why the average temperature on Earth is 0,9 °C. At least according to NASA, the authoritative US agency.
Meteorologists prefer to calculate with an average temperature of part of the thin atmospheric layer in which people live. They omit the polar regions from their calculation and thus arrive at an average temperature of about +12 °C(1), or +15 °C in a slightly different layer. It doesn't matter if you assume one or the other, both are amazingly high!
I will try to explain why this is surprisingly high. The Earth must be a kind of greenhouse that retains heat. We just don't know how that works. Rumor has that it is because of the atmosphere, which contains "greenhouse gases". In particular CO2, part of which we humans discharge into it with our fossil fuel consumption. However, it is not nearly that simple. Our CO2 is nothing more than an extra drop in a half-full bucket. What we do know is that we constantly receive a lot of energy from the sun. For temperature balance, we have to get rid of that energy and that can only be done by radiating it to the universe again.
Input and output radiation are approximately the same, on average.
The temperature of Earth
The temperature in the interior of Earth is about 5000 °C. The fact that we do not burn our feet is because the Earth's crust conducts heat very poorly. We notice so little of it on the surface that we can neglect it compared to the heat we receive from the sun. A little bit of that geothermal heat does escape, but that doesn't make it any colder inside. The loss is supplemented by radioactivity. Our Earth is a kind of nuclear reactor, which keeps the interior temperature steady. It has been doing this for 4 thousand million years. When we talk about the temperature on Earth, we therefore only reckon with the energy of the sun. And as far as that tiny bit of geothermal energy is concerned, this is also constant in the human period. Radioactivity is insensitive to temperature or gravity.
Greenhouse, and the geotriad
Now for the greenhouse effect. How big is that actually? Books and publications often state that Earth's temperature would be on average -18 °C if there would not be a greenhouse effect. That is not true. It is the result of a common error in calculations. One averages first and then calculates. While the opposite must be done. First calculate and only then average.
Without a greenhouse effect, the average temperature would be -128 °C(2). That is the average temperature a stone sphere would have in our orbit around the sun, if it did not equalize the received solar energy around the sphere. The sun does not shine everywhere with the same power and not at all at night. So it does not get equally hot everywhere. With full equalization, the sphere would always and everywhere have the same temperature, -18 °C. With no equalization at all, every point on the surface has a temperature that is exactly as high as necessary to radiate the received energy back to the universe. In that case the temperature in place and time is unequal and on average -128 °C.
The degree to which the sphere equalizes temperature is therefore extremely important for the temperatures that you would measure there. 1% more or less temperature equalization can make a 1 - 2 degrees difference.
So, the first step in understanding Earth's greenhouse is knowing to what extent the Earth equalizes its temperature. We know that it is not the same everywhere. On the solid surface the temperature is sometimes -70 °C in some places. In other places +55 °C. And the ocean (70% of the Earth's surface) is significantly warmer at the equator than at the poles.
A theoretical sphere in our orbit around the sun, which itself would not uniformly distribute the energy received, but which would have to radiate that energy locally and at any time in order to get rid of all that energy again, would have an average temperature of -128 °C(2,5).
The Earth's energy transport is part of the total greenhouse effect. If it were ideal, that is, if the shell radiating to the universe were always and everywhere at the same temperature, it would raise the radiative equilibrium temperature from -128 °C) to -18 °C.
It goes without saying that the terrestrial energy transport is not ideal. Otherwise it would always be equally warm everywhere. The actual radiation equilibrium temperature is therefore somewhere between these two extremes. No one knows what it really is. I estimate that the heat transport is so good or bad, that the actual terrestrial equilibrium temperature is around -70 °C. To get to the 0,9 °C of NASA or the +12 °C or +15 °C for the inhabited layer of our weather guys, there are still many unexplained degrees to bridge. Many more than the 30 °C from -18 °C to +12 °C, for which CO2 in the atmosphere is given the leading role in the current discussions worldwide.
Which physical processes ensure that we do not live on an Earth where it is -270 °C at night and where we cook to death in places directly under the sun? And are those processes equally strong everywhere and at all times? Is there reason to believe that they will not change except by burning coal, oil or gas?
I divide the total greenhouse effect into three main groups, the geotriad:
- The energy transport over the Earth's surface and atmosphere by ocean currents and air movements. This to some extent equalizes the uneven temperatures that the sun alone would produce.
- The storage and release of energy in the form of heat by the ocean and soil (plus vegetation and buildings). Due to the rotation of the Earth and the orbit around the sun, this has a leveling effect on temperature differences.
- The turbid properties of water and air and their heat storage. As a result of this, the shell radiating stored thermal energy (heat) to the universe must necessarily have a lower temperature than the layers below it. The heat storage and release of the soil and the ocean also do this independently of the influence mentioned under 2.
As with everything in nature, where many factors play a role, one of them is responsible for changing the whole only if all other factors remain constant.
Since CO2 only plays a role in the third part of the geotriad - due to its influence on the transparency of the atmosphere - and is not the only one there, the assumption that everything else is changeless is a rather bold assumption.
In addition, the influence of the sun is not necessarily changeless(3).
Triad factor 1, energy transport over the Earth's surface and atmosphere
We do not live on the Earth, but in a layer. We are therefore not bothered by the Earth's inner heat of 5000 °C. The thickness of the shell that is important for our well-being is no more than a few tens of kilometers. (The radius of Earth including the noticeable atmosphere is about 6600 km; the tangible Earth radius is about 6300 km with an additional 300 km for the atmosphere.)
The incoming energy from the sun is partly reflected. Reflection does not affect the temperature of a medium it hits. In our shell we therefore have to deal with a solar flux of approximately 1000 W/m2 (Watt per square meter perpendicular to the radiation direction). That 1000 W/m2 only enters our shell at a place where the sun is directly above. At other places it is less. At night and at the poles it is zero. (Strictly speaking, the latter is only true around March 22d and September 22d and during winters around the North and South Poles.)
To keep the temperature averaged over a year constant, Earth must get rid of the incoming energy during the same year. This is only possible through radiation to the universe. Without any Earthly energy transport in the atmosphere, ocean and ground, an average temperature of the Earth as emitter of -128 °C would suffice for this. With ideal transport, i.e. the Earth as a whole, having the same temperature everywhere and always, this would be -18 °C(4).
A 110 °C temperature difference is quite something. This shows that the way in which the Earth itself distributes the received energy has a huge effect. And this should, with a small change over time in the transport properties, make a significant difference in the temperature of our shell. Energy transport is therefore a major factor in the total greenhouse effect.
Warm water (70% of the surface) flows to colder places, as does warm air. Cold water and air cool the warmer areas. All of this makes a significant contribution to the redistribution of the received solar energy. Measured temperature differences between day and night, for example, are not very large in many places.
But are those flows constant in time on average per year over a longer period? We know the ocean movements are not constant. There are cyclical variations like El Ninjo and El Ninja, about which we have recently learned a lot. But aren't there other changes over a long series of years? Much less is known about this. We also know that winds are far from constant. But do they change when we look at annual averages? We don't know enough about this either.
Many assume that the changes will average out over a number of years and that it is reasonable to assume that a constant energy transport can be assumed for the climate, in which 30-year periods are calculated. I note that this is an assumption which can only be verified with very accurate measurements over a very long time. As long as this is not the case, it must be considered that there may be changes. Immutability is not certain. 1% change in energy transport over a century can mean a 1 to 2 °C temperature difference. And the energy transport of the flowing water is an important part of the total energy transport of Earth. I suspect the effect of the air to be less, because of its low heat capacity and its variability; although it travels with higher speed. (The energy transport from moving air is very important for the local weather, which are processes of days or weeks. But that is different from the long-term climate.)
Trias factor 2, storage of energy by the ocean and the ground
Another factor that regulates the temperature distribution over place and time
is the storage and release of energy in water and soil on a rotating Earth in a
seasonally dependent position with respect to the sun. The radiant energy, which
water and soil mainly convert into heat, is transported by these movements to
other places relative to the sun. The stored energy in water and soil does not
only remain at the surface where the radiation enters. The gradually absorbed
radiation energy follows a
way out from where it was stored. This happens by heat conduction and
convection transport between deep and shallow layers. Due to transport
resistance, it arrives at a different location with respect to the sun. This process
also accounts for an important fraction of the Earth's energy transport, which
determines our radiation equilibrium temperature between -128 °C and -18 °C.
Although its immutability is not certain, I consider the assumption plausible that it does not change measurably in terms of its influence on the climate. But we don't have any certainty. It is uncertain to what extent buildings, land use, including vegetation, influence this energy transport.
In summary, this temporary energy storage of soil and ocean in connection with the Earth's motion is also a factor of importance for the temperature distribution and thus for the radiation equilibrium temperature. It is a significant part of the global greenhouse effect.
The processes summarized in the aforementioned two factors increase the theoretical radiation equilibrium temperature from -128 °C to somewhere between -128 °C and -18 °C. That is not enough to understand why the temperature in the inhabited layer has a value as measured and mentioned in the Introduction. Some authors, including me, suspect that that the temperature of the layers ultimately taking care of the radiation to the universe, is not very far above an average of -73 °C. The actual value depends on the radiation properties of those layers and their temperature distribution.
Triad factor 3, the turbid properties of water and air and their heat storage and release, including those of the solid soil
The measured temperatures in the layer we inhabit also depend on processes summarized in the third factor. Many consider the atmospheric blanket, that hinders energy flow, to be responsible for this. But that is too short-sighted. In the climate literature we often find an explanation in which only a temperature difference of the incorrectly calculated -18 °C to +12 °C needs to be bridged. And that would be due to greenhouse gases in the atmosphere. It will be clear from the foregoing that the gap still to be bridged is larger.
So there is more to it. If the models showing a temperature increase due to greenhouse gases were correct and would explain an increase of 30 °C, then the question still remains, what causes the temperature difference between the partial temperature equalizing factors 2 and 3 (-73°C??) and the -18 °C?
One of those processes is the result of the turbid properties of air and water. In a turbid medium the radiant energy penetrates further than the surface before it is completely converted into heat, (thermal) energy. Certainly, this energy cannot be transported back to the surface by radiation through the ocean, 70% of the tangible surface of the Earth. The wavelength of the radiation produced by matter at the prevailing temperatures is prohibitive. For that radiation, water is completely opaque, or 'pitch black'. The heat must therefore be transported through convection and conduction. And that can only be done from warm to cold.
So, inside a turbid body - the scientific name is "diathermal body" - the temperature must be higher than at the surface, where it is passed through evaporation, conduction, convection and radiation to the next layer - the air - on its way to truly extraterrestrial.
In the water, this transport is also slowed down by the warming from red and infrared sunlight absorbed close to the surface. Measurements confirm this, see the figure below.
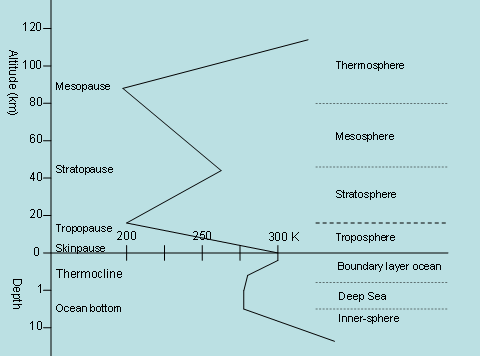
The temperature distribution with height and depth [km].
Something similar takes place in the air. The infrared radiation from the ground and water surfaces is partially absorbed by greenhouse gases and converted into hot air. Air contains fewer molecules per m3 than water, but this conversion also takes place here. It is mainly taking place in three- and polyatomic gases such as water vapor, H2O and CO2. The air transports by radiation only part of the received radiant energy and the rest must be moved away by heat, which requires a temperature gradient. The bottom layer of air must therefore necessarily be warmer than the higher layers. Only when the air density is so low that the radiation transport experiences less hindrance, while the other transports become smaller due to lack of mass, a temperature gradient is no longer required for energy transport. The heat effects in turbid matter are comparable to energy transport in a bed with an electrically heated underblanket.
Into such a bed, an electrical cord transfers energy unhindered, comparable to deeply penetrating solar radiation, in the ocean and atmosphere. If you put a thin sheet over that electric blanket, the bed will heat up until as much heat escapes through the sheet as the electrical energy brings into it. If you cover the bed with a thicker blanket, the bed will become warmer. A higher temperature inside is needed to push the heat out.
The long-wave radiation from the tangible Earth also penetrates the air a long way before the greenhouse gases have converted a substantial part into heat in layers of air. And if that energy is emitted as radiation, it is captured again after millimeters, meters or kilometers and converted into heat.
Anyway, turbid properties make a medium warmer internally than an opaque body would become in a radiation field(5).
The solid ground warms up when the sun shines on it. The surface reradiates some of that energy. Part of it is released into the air as heat energy. Another part is transported as heat to the subsoil. That part can only be removed again when the surface is colder than the ground at night and in winter. All these processes slow down energy release. And they have in common that the soil is on average warmer than an opaque medium would be if it did not retain and conduct heat. Such a medium should, when receiving solar energy at its surface, immediately release it again into the air by radiation or heat transfer in order not to continue heating up indefinitely. For heat transfer to the air it is also necessary that the ground surface is warmer than the air.
Heated water also releases its energy, but in a different manner. It is done via heat transfer to the air, which requires a temperature difference, and by evaporation. The energy required for evaporation is returned to the air up to a fairly high altitude. That transport is important. It takes place over great distances. The average over the whole year and the entire Earth's surface is 71,5 W/m2. (There is about 1 m of precipitation on Earth per year and the heat of evaporation of water is 2256 J/g.) Climatologists assume a (similarly average) incoming solar energy of 161 W/m2. They even estimate 85 W/m2 needed for evaporation. My calculation is therefore on the economical side. This process of energy transport back to space alone accounts for half of the incoming energy from the palpable Earth. And it requires a temperature gradient. They also calculate with an average heat emission to the air of 20 W/m2, which also requires a temperature gradient.
All in all, this is an energy transport driven by temperature difference, which does not involve any greenhouse gas. But even without an atmospheric greenhouse effect, this energy transport causes the layer where we live to be warmer than the part of the Earth that ultimately keeps Earth's energy content stable through radiation. It is therefore also part of the total greenhouse effect.
Discussion and conclusion
Yes, our litle residential layer on Earth is a greenhouse. It stays at the right temperature due to the sun and the geotriad. Without the triad it would be 143 °C colder. That triad heater deserves more attention than it currently receives. Admittedly, we know quite a bit about the array of processes that make us live comfortably like greenhouse plants. But that knowledge is not accurate enough to know how much each of them is doing and whether they are stable.
Atmospheric processes play a role. Greenhouse gases in the atmosphere as well, but a smaller role. And among them, CO2's effect is not the strongest. Water vapor, H2O, is more important and we cannot influence it. We also do not know whether those gases together make a 30 degrees difference. The proportion of everything else is insufficiently known for that. According to CO2 radiation expert Witteman(6), doubling atmospheric CO2 leads to a temperature increase of at most 0,2 °C. Others tell us it is more than 4+ °C.
With so much uncertainty in the so intensively studied change, in addition to the much greater uncertainty about the rest of the geotriad, welfare-destroying CO2 measures are irresponsible. Moreover, if those others are right, they will make a difference of less than 0,2 °C on the 143 °C in question in 80 years.
Acknowledgement
I am grateful for the help of Albert Stienstra with the editing of the English text. Remaining flaws are mine.
C. (Kees) le Pair
Nieuwegein, 2020 09 19.
2021 05 03 adjusted following comments by
Chr Schoneveld, A. Bijkerk & H. Matthijssen,
G. Goltstein & A. Stienstra
Last correction 2021 11 13.
Notes
- Physicists prefer to measure temperature in units K, the abbreviation for Kelvin. A temperature of 273,15 K equals 0 °C. The absolute zero of the temperature is 0 K or -273,15 °C. The temperature of the universe is 3 K (-270 °C).
- I once figured it out, assuming every scientist had known it for a long time: KLIMAAT,
STRALING EN TEMPERATUURVEREVENING-2. This applies to physicists, at least when they have thought about it. But it does not seem to have penetrated everywhere in climate science.
- Since this lesson is about the greenhouse, I will not discuss changes in the sun and the shielding and reflecting by clouds. These too can have consequences for the Earth's climate.
- The difference is due to the fourth power in Stefan-Boltzmann's radiation law. See note (2) and my comment about calculating with averages instead of calculating first and then averaging.
-
RADIATION BALANCE AND TRANSPARENT MEDIA - 3; Principia Scientific International, 2018 12 03. Or here in Dutch.
- W.J. Witteman: The Absorption Of Thermal Emitted Infrared Radiation By CO2. The article can be downloaded here as a PDF file.
|
|




