The impact of wind generated electricity on fossil fuel consumption.

clepair@casema.nl
kenjdegroot@mac.com

Abstract

Wind turbines produce electricity which is delivered to the grid. Variations in wind velocity cause yield variations. Conventional power stations are forced to compensate these variations by adjusting their output. This has a negative effect on the efficiency of the latter stations. Using data provided by CBS, the Dutch Institute for Statistics, an estimate is made of the so called “turning point”. This is the point where the efficiency reduction of conventional power stations balances out the fuel saving of the wind turbines, and where the CO₂ emission reduction turns negative as well. In the Netherlands the data for the year 2007 show this to be the case at an efficiency reduction of all power stations of about 2 %. The Dutch government uses an incorrect formula for calculating the fuel and emission saving from wind energy. On this subject parliament has been incorrectly advised by government.
In addition, fuel costs required for initial installation of wind turbines are substantial.
Application of wind energy without adequate buffer and storage facilities serves no green purpose.

Introduction

In a previous article¹ we calculated the negative effect on the fossil fuel saving obtained when using wind generated electricity. The effect is caused by the stochastic nature of wind availability, which requires frequent and rapid output adjustments of the fossil fuel powered plants. In our sums we used German data, because wind turbines have been erected there in large quantities. We also used somewhat too high estimates of the efficiency of fossil fuel power stations. We now turn our attention to the Dutch situation, where thanks to our CBS, the National Bureau of Statistics, actual data on the fuel input and electricity output of various kinds of power stations are available.
 Coupling wind farms to the electrical power grid requires additional output adjustments of the other power stations to allow for wind fluctuations. We will call these other power stations “conventional producers”. Without wind farms these producers would provide an amount of electricity E according to demand. This would in turn require an amount F of fossil fuel. The efficiency is then equal to

R = E/F

(1)

Now if the wind farms produce an amount of electricity E_w and demand remains the same, the conventional power stations will need to produce E-E_w.
The Dutch government² and public conclude that the fossil fuel saved ΔF can be related to the efficiency and the total fossil fuel use of the system as follows:

F - ΔF = ( E - Ew) / R

(2)

with ΔF=E_w/R. This leads to an equivalent lower amount of CO₂ production. This is incorrect. Wind energy is not supplied in response to demand, but fluctuates with the weather. This requires the conventional power suppliers to more frequently adjust their output up and down, in order to balance the fluctuating wind generated electricity supply. As a consequence, the other power stations will have to run at below optimum generating capacity more often. This leads to an efficiency decrease from R to R-ΔR.
The amount of fossil fuel used in a situation where wind is providing electricity as well thus becomes:

F - ΔF = ( E - Ew) / ( R - ΔR )

(3)

and the fuel “saving” ΔF is equal to:  

ΔF = F - ( E - Ew) / ( R - ΔR )

(4)

ΔF can become negative, and then wind power does not save fossil fuel, but causes extra fossil fuel consumption and also extra CO₂ emission. The turning point where no fuel is saved is reached when ΔF = 0
When combining equations (1) and (4) for ΔF = 0 we find:  

E/R= ( E-Ew) / ( R- ΔR )

and therefore

ΔR = Ew*R/E

(5)

 Thus, at a (conventional power) station efficiency of 50% and 5% of total electricity generated by wind, the turning point ( = no fuel or emission saving during wind farm operation) is reached at a total conventional power station efficiency loss of 2,5%. Again: the loss is caused by having to cope with extra demand fluctuations.
Generally the following equation holds for the efficiency loss at the turning point:

(ΔF = 0 if) ΔR = aR

(6)

with

a = Ew/E,

(6a)

a being the fraction wind generated electricity on the total production. Note that the duty factor (= also called: wind turbine efficiency or capacity factor), the fraction of the name plate capacity delivered in a specific time period, is absent in the equation.

Reality

Does an efficiency loss of this magnitude actually occur? We were unable to find data on this effect. In our earlier article we called this “ a well-kept secret”. We did receive promises from researchers that they would try and send us the relevant information. So far, we have not received data. Electricity producers, apart from EPZ(Zeeland), have not provided us with the information. Again, we have received promises that this will be subject of study.
 F. Udo³ has made estimates on the basis of performance data of various generating units. These estimates show negligible overall fuel and emission savings during wind farm operations. He also focusses on the technical (in)ability to fit in the wind generators in the overall system.
 B. Chr. Ummels sees no difficulty for this fitting in of wind power, even when the Dutch wind generating capacity would be 12 GW (Ph. D. thesis⁴ Delft University). Udo shows however, that according to Ummels' own calculations (in his figure 2.12, ibid.) either the conventional power stations or the wind farms have to be switched off for about half of the time. This of course destroys the security of electricity delivery. Udo estimates the average efficiency of the Dutch conventional power stations to be 50%. The actual figure for the year 2007 is about 43,5% (see below). Comparing these two figures gives an indication of the effect of running below peak efficiency or at variable load. An efficiency loss of about 2% caused by fluctuating wind supply is therefore not unreasonable at all. The effect of such efficiency loss is, however, that no fuel or emission reduction occurs at all.
 J.Soens⁵ calculates – in the same way as done by Ummels that for the Belgian situation a maximum wind contribution can only be 700 MW (17 times less than Ummels' goal) to reach the point beyond which adding wind farms becomes counterproductive.
 In the spring of 2009 a Delft group published a report⁶ in which the efficiency loss due to wind power addition to the grid was mentioned, but not quantified.
 Kent Hawkins⁷ recently published a study of the technical characteristics of gas powered electricity generators, which are used for back-up of other units. He concluded : “The general conclusion is clear: industrial wind power does not produce the claimed benefits of reductions in fossil fuel consumption and CO₂ emissions when up-and-down backup generation inefficiencies are taken into account.”
 W. Katzenstein and Jay Apt⁸ address the emission of CO₂ and other gases as a result of rapid output change of natural gas fired generators. As far as we can make out, their study does not consider the effect of having to replace the slowly reacting, but efficient generator systems (efficiencies up to 58%) by the quickly responding but inefficient (about 30%) gas turbines. Nevertheless, they find that the quick ramping up and down of the gas turbines leads to a reduced (75-80%) emission saving compared to the one expected when this effect is not taken into account. We note that CO₂ emission is roughly proportional to natural gas consumption.
 The Dutch Ministers of Economic Affairs and of the Environment replied to questions in Parliament on February 10 2010 on this issue. Their answer contains the following passage: “ When wind electricity is supplied, conventional power stations will step down their power, and also use less fuel and emit less CO₂, to allow for the use of wind electricity”. They also state that, on the basis of “verified” numbers, a reduction in output by 1/3 leads to 31,6% less CO₂ emission. They have not indicated how these figures were verified. That is impossible anyway, because in the report from the Delft group, that they quote⁶, this information is not provided. A simple model calculation for an existing modern, rapidly responding combined cycle power station of known performance characteristics shows that an output reduction of such magnitude causes an efficiency decrease from 55% to 40%. In that case the fuel saving is about zero, as is the CO₂ emission reduction. The Dutch parliament has thus been informed incorrectly. May be members of parliament should directly contact the Delft group.
(New questions by MP De Mos, were answered in March. The ministry sticks to its wrong arithmatic. It does recognize the occurrence of efficiency losses¹⁴.)

  People and organizations go a long way in defending wind farms. NUON, a Dutch electricity provider running an offshore wind farm, renovated a number of old (inefficient) gas-fired power units to cope with the rapid wind variations and its consequences for the electricity supply⁸. Udo (op. cit.) provides an interesting analysis of the resulting effects. Anyway, one keeps stations in operation with low efficiency and thus high fuel use and emissions rather than reducing fossil fuel use and emissions by upgrading to more efficient units.

The Netherlands

The Netherlands uses various power sources for electricity generation. Most use fossil fuel. The share of each power type is presented in table 1.

In the first row, the Total Supply includes the nett result of import and export. Because the Netherlands was a nett importer this resulted in electricity without fossil fuel expenditure and thus a higher overall fuel efficiency. The import only costs money, but that is not under consideration here.
The second row, national production eliminates import, but includes the (“non-wind”) sustainable component. This sustainable component is probably not required to adapt to wind fluctuations.
The third row national Production incl wind, excl sustainable is probably the most desirable mix to adjust to the wind fluctuations if this could be organized with so many suppliers, each with their own fluctuating demand. A Smart Grid could help accomplish this.
The fourth row eliminates the decentralized generation, thus painting the situation where such generation is not involved in compensating for the wind variability.
The next rows show the large power stations with and without the single Dutch nuclear power station. The latter has not been required to help out against the wind variations. It remains at full power as long as the electricity demand in the country is larger than the so called 'must-run' level¹⁰. This power station increases the pseudo fossil fuel efficiency of all large power stations incl. wind with ± 2,6 %. The turning point is hardly affected.

Discussion

These calculations indicate how small the overall efficiency decrease of conventional electricity production needs to be to reach the point where no fuel is saved or CO₂ emission reduced in the case when these conventional power stations are required to compensate wind electricity variability. Obviously, wind variability can be larger than that required to reach the turning point and in such a case wind energy leads to increased fossil fuel use and CO₂ emission.

 Let us also bear in mind that the building, erection and maintenance of wind turbines requires fossil fuel as well. The turbine steel and other material and the (concrete) foundation require energy for their manufacture. A wind farm requires a conventional power station with a power equal to the maximum power of the wind farm. A wind farm with a 25% duty factor requires a back up station with four times the power of that belonging to the actual electricity produced by the wind farm. A critical analysis of the pay back time of the wind farm fully accounting for all fossil fuel expenditure in its manufacture, operation, maintenance and back up requires another study.

 Our preliminary estimate, based on data from J. van Oorschot¹³ shows the energy pay-back time to be minimally 1,5 years. This period is a very optimistic minimum. In this estimate the energy costs for the manufacture of the back up units, the extra high tension grid, transformers and regulating systems etc. The Dutch Gasunie, managing the natural gas distribution grid, announced in December 2009 to plan extra gas pipelines, amongst others because wind energy requires so much extra natural gas. In our estimate we have used the overly optimistic output formula used by the Ministry of Economic Affairs which we have shown here to be wrong. In addition one has to account for the fossil energy costs of maintenance of the turbines, which especially in the case of offshore placement will be significant.

 It is quite conceivable that the efficiency reduction of the conventional power systems is not noticed by the operators. Wind electricity has as yet only a tiny contribution in Holland: only some 3,3% of the national electricity production and therefore less than 0,3% of the national energy use. (Do bear in mind that the amount of conventional back up required is about 4 times as large). The wind contribution has grown rather smoothly, and thus the resulting efficiency decrease is also slowly growing. In the period of wind turbine capacity addition conventional installations have probably been replaced by more efficient ones. This may well have masked the negative effect of the wind turbine addition. As an example, dual cycle gas turbines run at almost 60% efficiency, although it takes about one hour before this level is reached. As long as the steam cycle is not operational (i.e. during this hour) these machines run like open cycle gas turbines at 25 to 30% efficiency.

 In figure 1 the development of the efficiency of fossil fuel driven power stations is shown for the period 1998 to 2008. The CBS figures for the years 2007 and 2008 are provisional. (There is also a difference between tables, but within one table there is consistency.) It is clear that the efficiency is not a stable quantity. It can only be calculated 'after the fact' and without detailed additional data from the producers the cause of the variation remains unknown.

Figure 1

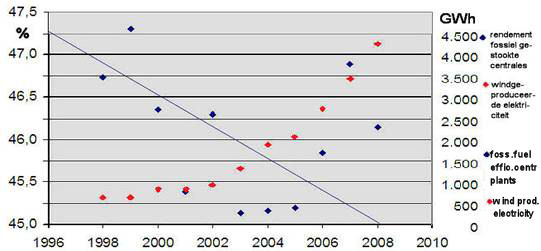
Efficiency of fossil fueled plants &
amount of wind produced electrical energy.
Drawn line represents decreasing efficiency trend,
neglecting the 'not yet corrected' years 2007 & 2008.

In an earlier paper¹ we proposed an algorithm to calculate the effect on the overall efficiency of all conventional power stations while only part of the powerstations effectively are required to back up the wind turbines. We start from the equation:

E = Ew + Ebu + En

(7)

in which E_bu is the amount of electricity produced by the back up units, and E_n is the amount of electricity produced by the power units that can work without disturbance, i.e. as if no wind variation needs to be compensated. The fuel use when wind electricity is added is now equal to the sum of the undisturbed and the disturbed conventional production, and with formula (3) we can write:

(E - Ew) / (R - ΔR) = Ebu / Rbu + En / R

(8)

When the duty factor of the wind turbines is equal to b, one requires conventional capacity to deliver in case there is no wind to the tune of E_w/ b. Overall, the back up system only has to deliver E_w / b - E_w Because E_w = aE we get:

Ebu = aE(1 / b - 1)

(9)

En = E - aE - aE(1 / b - 1)

(10)

Inserting (9) and (10) in (8) one gets at the turning point (no overall saving), where ΔR = aR:

(ΔF = 0 if) Rbu = R(1 - b)

(11)

This critical efficiency value of the back up units at the turning point is independent of the fraction of the wind generated electricity, but directly related to the 'duty factor' of the wind turbines.

 In the Netherlands in 2007 a = 4,63%, and we assume b to be 25% .(This is more favourable than in Germany, where the nation-wide value for b was on average over several years about 17%, with variations over the years from 14% to 21 %.) The turning point in Holland is therefore always some 75% of the average 'normal' efficiency factor. The result of the calculations is shown in table 3, where we show the overall efficiency reduction ΔR versus the efficiency of the actual units doing the back up.

 Table 3 demonstrates that at a hardly noticeable efficiency decrease for the overall system (Small compared to the yearly fluctuations in this overall efficiency number.) the stations effectively providing the back up are operating at the indicated reduced efficiencies. In case all back up for wind farms in Holland would be provided by open cycle gas turbines, having a 25% to 30% efficiency only (Electricity producer NUON is doing this for its offshore wind farm), in 2007 we would have been beyond the turning point. Under the same conditions as in 2007 (same b, same total of electricity supply, but with twice the amount of wind electricity and consequently less conventional contribution), the R_bu threshold would remain ~ 34% and again there would be no saving. More fuel would be burned and more CO₂ emitted than in the case where no wind was being used. Pay-back of the energy spent during construction and being spent to run the extra kit is obviously out of the question.
The conclusion is independent of the wind contribution: If the wind contribution is n times larger, the turning point remains at R_bu = 34%.
At 9% wind electricity the power stations held hostage by the wind is already about ~41% of the total conventional capacity

 We have also calculated, using formula (4) how much fuel is saved for the 2007 wind energy production of 0,39 GWyr when using different realistic back up configurations. Figure 2 presents the results, being the fuel saving ΔF as a function of the efficiency decrease ΔR. It is shown that in all configurations the fuel saving turns zero when roughly 2% efficiency is lost due to forced output variations to compensate for wind variability.

Figure 2

ΔF [GWyr]

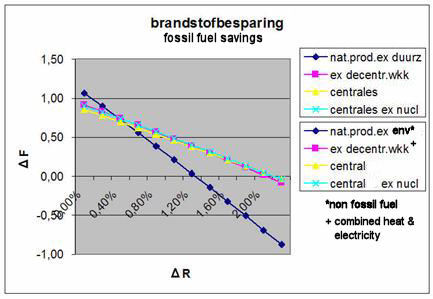
Fossil fuel savings as a function of
decreasing efficiency for different
'back-up' strategies.

Conclusion

The use of wind energy for electricity generation in combination with the requirement for fossil fuel powered stations to compensate for wind fluctuations can easily lead to loss of the expected saving in fuel use and CO₂ emission. In addition, the conventional stations will be subject to accelerated wear and tear.
 It is recommended to get an accurate and quantitative insight into these extra effects before society sets out to apply wind energy on a large scale. Producers must be required to publish data on the efficiency, the wear effects and the fuel use when wind energy is added on.
 Economical energy storage and buffering methods are an essential prerequisite for large scale application of wind energy for electricity production.
 It is conceivable that the (counter intuitive) use of wind energy in the Netherlands to produce hot water rather than electricity is to be preferred if one wants to achieve the objective of reduction of fossil fuel use and CO₂ emission.

Nieuwegein/Leidschendam
2010 04 18.
Update-1, note 12.
Update-2, note 7, 2012 04 27.

References & notes.