>

COMPLEXITY, CLIMATE, CO2 AND ENGINEERS
Introducting tutorial for aspiring climatologists

Abstract

Complex systems have more than one actor, which influence each other. To understand them from the perspective of one dominant actor, some conditions must be met. Even if the actor itself is well understood, this leads to unexpected results in complex systems. A planetary motion serves as an example. The test of atmospheric CO2 understanding, temperature understanding and understanding of their mutual relationship, against those conditions is negative. Some understanding can be derived from practical research of the total system. Engineers, doctors and other professionals have been doing this for century's .


Content

  1. Complexity
  2. Planet orbiting
  3. Climate
  4. Temperature
  5. CO2
  6. CO2 and temperature
  7. Conclusion CO2-temperature
  8. Discussion and Engineers
  9. Thanks
  10. Notes


    11. 1. Complexity

    Complex is a commonly used word. It has several meanings(1). In natural processes there is an unambiguous description:

    A complex system is governed by several mutually influencing actors.

    Climate is such a system, as is the storage and transport system of CO2. (Numerous other systems are also complex.)
    We can sometimes describe a complex system based on one or more of the actors. At least if certain conditions are met. Later in this article I argue that this is not the case with climate(2) and CO2, and how we can deal with such things.

    1. The chosen actor must be accurately known.
    2. The effect of the action of that actor on the total system must be substantial compared to the noise caused by the other actors.
    3. The initial conditions, i.e. the state the system was in at the start, must be accurately known.
    4. The description of a dynamic process must take process times into account. (Often (equilibrium) thermodynamic considerations do not meet that requirement.)

    Feynman taught us: When a) is not satisfied, accurate and very strict mathematical calculations lead to crazy results.
    This also applies to the other conditions.

    For convenience, we often circumvent the problem by assuming that all other actors except one are constant and that the system can then be described with that one actor. That's wrong! Even then the others join in. That can give very counter-intuitive results.
    Since this seems rather abstract, I will give a concrete example.


    2. Planet orbiting.

    Tycho Brahe accurately mapped the planetary motion with his instruments without mirrors or lenses. Johannes Kepler derived descriptive laws from this. And Isaac Newton Newton explained all that from the mutual attraction of two masses. It turned out that the calculated movement of the earth around the sun was in agreement with the observations, but not exactly. That was because the moon and the other planets also attracted the earth. So they tried to "just" calculate the motion for three instead of two masses. However, that didn't work. In principle, Newton's differential equations cannot be solved for this.

    More masses exacerbate the problem. We can do it numerically. I.e. Starting from the initial state, we calculate a small step under the influence of all forces and then we calculate again with the outcome of the previous calculation as start, the next etc. We call this iteration. With the help of modern computers you can calculate the future state with ever smaller steps and many iterations with a limited certainty. But not exactly! It may beaccurate enough for many purposes.Yet it was not entirely within the calculated accuracy, when one could measure even better. The difference between measurements and the calculation at Mercury revealed that there was something wrong with condition a). The sub-process of attraction between two Newton's masses. Einstein's theory of relativity cleared that up. Now we can do it well, provided that we iterate numerically enough.

    Please note. Here we are dealing with a system whose sub-process - the motion of two masses - is exactly known, as is its initial state. For example, we now predict planetary movements this way. Recently, researchers did this for Mercury. They calculated her position after a long time. Then they repeated the calculation for the same period with the same iteration. They only chose a 2 cm offset starting position of Mercury. The outcome of the first calculation yielded a position at a point nearly on that planet's currently known orbit. The second calculation, however, taught that Mercury would be inside the sun at that time. A two cm changed initial position is of course negligible at cosmic distances. But the effect of the minute difference is dramatically different for this complex system. Mind: the margin of error due to the iteration was known to the researchers and, we can assume, small enough compared to the 2 cm. Hence the first result. But 2 cm "error" in the initial state makes a million times greater difference in the final state in this simple complex system.

    How can such a small difference grow into such a cosmic drama in the foreseeable future? A 2 cm shift will certainly not let Mercurius collide with the sun tomorrow. If, as a result of this shift, the interaction with its actors differs slightly, the influence of all actors is different. Also those of the actors, whom we kept constant for the sake of convenience.

    A calculation of the behavior of a system consisting of precisely known subsystems is called fundamental or 'based on first principles'. We are even satisfied if it can only be done numerically, because then we can indicate the margin of error in the final result.
    In the real world, complex systems seldom completely satisfy all the stated conditions. Nevertheless, you can sometimes reasonably describe the system on the basis of 'first principles', provided the conditions are approximately met. However, the uncertainty is much greater than by the numerical method alone, as we saw in the planetary example. If condition b) is less than half the noise, the calculation says less than a signpost, telling: One of these roads leads to your destination.

    Astronomy still has numerous uncertainties due to complexity. Prof. dr. E. v.d. Heuvel, astrophysicist, mentioned the star models as examples(3). There are also many actors there. Central to this are four coupled differential equations. (Much less than in climate models.) And the boundary conditions are fairly well known. "After more than fifty years of research in this area, we now have fairly good (numerically calculated) star models for stars of all kinds of masses. Still, we are far from understanding everything." He mentions examples and adds: "This star modeling problem is much simpler than that of the climate models. There are much more differential equations and many of the boundary conditions are not nearly as clear as with the star models."


    3. Climate

    Climate is a vague concept. It represents an average weather condition and is different for every place on Earth. Weather is a large collection of phenomena such as temperature, air pressure, humidity, wind, precipitation, etc. Places on earth with the same average temperature can differ greatly in average wind or precipitation, etc. and in the distribution of that temperature over the day or year. So there is no such thing as a global climate. Moreover, it is actually not about the global climate, but that of a part of a thin shell of the earth, in which people live(4). And Iraqis experience climate differently than Inuits.

    Discussion is therefore only meaningful about measurable phenomena, such as temperature, sea level, etc., the composition of the sea, air and soil and, above all, sun behaviour. The system in which they play a role is extremely complex. Descriptions must therefore meet the requirements for complex systems.

    A high-profile correlation is the relationship between temperature and atmospheric CO2. Each in itself a complex system, about which libraries have been written. These records do not always take into account the conditions that a description of a complex system must meet.


    4.Temperature

    Planets receive radiant energy from the sun. They themselves contain chemical and nuclear energy as well as molecular kinetic energy, which we measure as temperature. The simplest conceivable planetary system is a sphere that orbits the sun almost circularly and has no internal energy of its own. In a stationary state, it has to lose the energy received from the sun again to the universe. It does that by means of radiation. After deduction of reflection - reflected radiation goes straight back into space unused - that sphere must therefore have a temperature (higher than 3 K(5)). Because the sun does not shine on the sphere equally strongly everywhere and not at all on the night side, the absorbed energy differs from place to place. So also the temperature that is needed there to lose that energy again.
    The process has two extremes. One is that the sphere itself does nothing to redistribute the temperature evenly over its surface. In that case, every spot on the surface has exactly the temperature at any moment, which is necessary to lose the solar energy at that time.
    In that case, under terrestrial radiation conditions, the temperature averaged over the surface is 145 K(6)(-128 °C). The other extreme is a sphere, which continuously distributes the incoming energy evenly over its surface, i.e. has the same temperature everywhere. In that case, the temperature prevailing over the surface is always 255 K(6) (-18 °C) everywhere. Planets are complex, however, they only partially uniformize the temperature. Part of the uniformization takes place by rotation about their axis. Part of the energy received during the day ends up elsewhere before it is radiated. If they have an atmosphere in which the wind blows, and oceans that flow uniformize them too. These processes, like the degree of reflection, are subject to change, so that the energy flows are far from uniform in time and differ from place to place. Therefore, this simplest of all explanations for Earth's radiative equilibrium temperature teaches an unknown mean radiative equilibrium temperature at somewhere between 145 and 255 K(7).

    Meteorologists often refer to an average temperature of the habitable part of our earth's shell, which they derive from local satellite or other measurements. It is about 288 K (+15 °C). That cannot be our radiative equilibrium temperature. The difference from the maximum equilibrium temperature is called the greenhouse effect, due to the accumulation of energy before it is radiated. This is often attributed to so-called greenhouse gases in the atmosphere, including CO2. (Water vapor does more.).

    we know that the temperature is not uniform, the radiative equilibrium temperature is < 255 K. Since there is no uniformity, the greenhouse effect must explain anything higher than the actual radiative equilibrium temperature. We do not yet know, to an accuracy of fifty degrees, what the Earth's radiative equilibrium temperature is, so what the Earth's greenhouse does. While the Earth's rotation is nearly constant, its reflection and absorption are not. As a result, even that part of the greenhouse is not constant. And the ocean is important in the uniformization process through energy transport. That too is variable. Atmospheric infrared absorbing gas, especially H2O, CO2 and CH4, methane, influence both ingoing and outgoing radiant energy transport. H2O also does this via clouds (reflection). Furthermore, there is outflow due to mass transport and phase change. Energy transport is therefore an extremely complex system with countless varying actors. Thus, the question of whether the temperature, which is determined by a part of the energy flow, is fundamental - i.e. can be described with the aid of 'first principles', depends on the above conditions.

    In view of the aforementioned uncertainties, the subsystem terrestrial energy transport and thus temperature distribution is far from well known. So Feynman's warning applies here: accurate and very well thought-out mathematical calculations based on 'first principles' lead to crazy results.


    5. CO2

    Atmospheric CO2 is gaining a lot of interest as an actor in the Earth's energy transport system. Billions of years ago, the atmosphere consisted mainly of CO2, 500 million years ago it was only 0.5% (5000 ppM). In the last 400,000 years during highs of four interglacials it was still 0.03% (300 ppM) and now 0.042% (420 ppM). At the end of the last ice age it was only 0.018%(8). CO2 is not conserved. The amount changes by chemical conversion; it dissolves in water, is converted by bacteria and plants into other chemical substances, which partly recirculate it later. People do that too. They give nature some of the CO2 back. Insects do that better, they annually release ten times as much CO2 into the air as humans with all their machines.
    The countless processes that remove or add CO2 from the air all have their own process time. CO2 dissolved in the ocean dissociates to the extent that it depends on temperature and salinity. Part is converted into carbonates, lime and rocks, which also degas. Such processes have process times of millions of years, many millennia, and centuries. There are also processes that take much shorter time. A tree that forms a leaf, which loses it in the winter, after which it rots, removes as much CO2 from the air within a year as it puts back in. If he builds branches from it or his trunk, he can hold it for decades to centuries. And if that trunk falls underground and nature turns it into coal, it can take longer than 100,000 years before someone turns it back into atmospheric CO2 and returns it to the air. The interior of the earth also contains carbon-containing compounds, which gradually or occasionally end up in the air in the form of CO2 via volcanoes.

    The Global Carbon Project is a large international collaboration of researchers that is trying to map the CO2 system, storage, transport and conversion(9). The emphasis is on the influence of humans. The project encounters complexity. It hardly meets any of the conditions set. And much of the research is focused on one or more of the sub-processes mentioned above. So there is no hope for real understanding of carbon storage and movement from such deficient sub-process knowledge.
    This does not mean, however, that no phenomenological knowledge of the system can be obtained for a limited period of time. dr. A. Huijser and I did this for the atmospheric CO2 amount and the CO2 from fossil fuel(10). We do not pretend to understand the system. We have only shown that from data of the carbon converted by humans with a precision of ~1 ppM the atmospheric concentration can be calculated in the period 1880 - 2020. We venture a prediction for a period not more than the next 60 years, because of the complexity of the system.
    The CO2, or rather the carbon balance of the earth will remain a mystery for a long time to come. And fundamental understanding, assuming all sub-processes known is not in sight.


    6. CO2 and temperature

    CO2 in the atmosphere absorbs infrared radiation, emits it itself in all directions and thus warms the earth. It converts most of the absorbed radiant energy into heat. Most of that heat ends up in the inhabited shell. This is the influence of CO2 on the temperature; which disturbs society.
    Physically, this statement is meaningless as long as there are no numbers attached to it. There are plenty of numbers, both about what CO2 does to bring the radiation equilibrium temperature to the current value in that housing shell, and about what more or less CO2 means for the change in the current temperature. The results of all these studies differ drastically from each other. The cause of these differences is the complexity of the system. Some studies give slightly more weight than others to some involved subsystem or to the effectiveness of the CO2 in the atmosphere itself. Since there are countless actors other than atmospheric CO2, it is again a question of how one of them influences the behavior of the system itself. The actors also influence each other, so it is a complex system at its best(11).
    And so we have to check whether an explanation satisfies the complexity conditions.

    Condition a) concerns the accuracy with which the understanding of the subsystem of this actor itself is known. This has therefore not been met, given the different results of the studies. A counter-argument that all but one of those studies could be wrong and if we were to use the right ones, so we know this subsystem well, is not supported by the majority of climatologists and in the IPCC, the international climate panel. That publishes a spread of 2 - 8 °C for an uncertain CO2 increase until the end of this century. Prof. dr. W.J. Witteman does not get higher than a few tenths of a degree with CO2 doubling(12) (!). The uncertainty for a system that has risen 1.3 °C in temperature over a century and a half is too great to accept CO2 as a fully known actor.

    Condition b) requires a significant contribution of the subsystem in the noise altogether. The magnitude of the noise in the measured temperature depends on the period and the location over which instantaneous, local temperature measurements are averaged. Locally we have day and night differences of 50 °C. The uncertainty over millions of years as a result of ideal temperature equalization or no temperature equalization at all has a spread of 110 °C. Even if the part of the Earth's rotation in the equalization may be subtracted, a noise of about 50°C remains. When averaging over decades, the ice core measurements show a noise of 12 °C over the past 400,000 years. Monthly averages of our residential shell show a spread of ~0.5 °C. (See the satellite measurements for the period 1970 - 2022 in figure 1. Annual averages also fluctuated in that size during that period. The 'first principle' calculations of the influence of CO2 influence on temperature change are about 'the climate', for which climatologists agree to choose a period of 30 years. They are therefore only significant if CO2 as an actor would be accurately known. This is certainly not the case with the inaccuracy described under a).

    Fig. 1


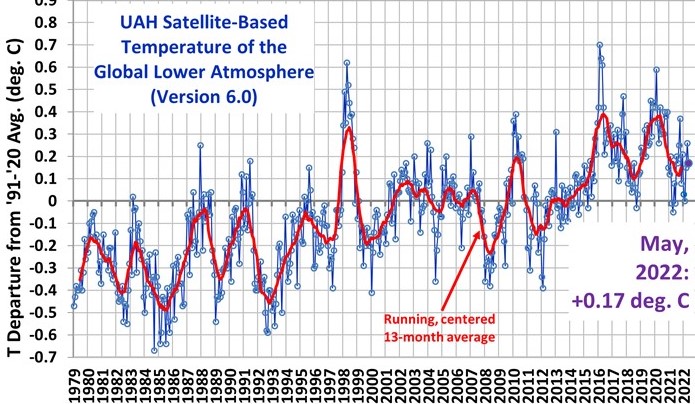
    Fig. 1. Monthly and annual temperature variation with respect to the average over the period.


    The 'first principle' calculations of the influence of CO2 influence on temperature change are about 'the climate', for which climatologists agree to choose a period of 30 years. They are therefore only significant if CO2 as an actor would be accurately known. This is certainly not the case with the inaccuracy described under a).

    Condition c), the initial conditions for the temperature of the housing shell are unknown millions of years ago. For this, this condition is not met. The temperature of the residential shell can therefore not be controlled by means of 'first principle' from the CO2 actor.

    The situation is different for the change in temperature in a short period of time behind us. It has been fairly well known since 1979. From that year on, calculations on the CO2 influence have been visualized by John Christy and Roy Spencer in figure 2.

    Fig. 2

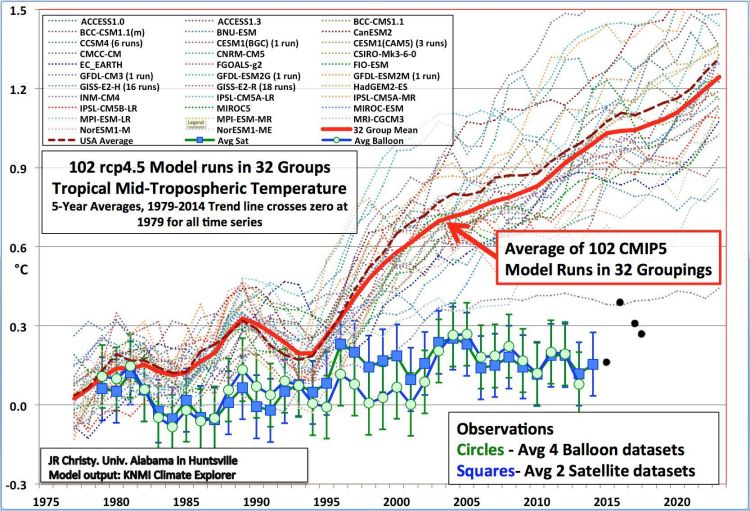
    J. Christy: Dotted lines indicate the first principle calculations of the temperature change due to changes in atmospheric CO2 concentration since 1979 and the measured data(13).

    Even with reasonably known initial conditions, the first principle calculations already deviate significantly from the observations after thirty years. Known initial conditions do not even aid understanding of temperature changes.

    Condition d), Process times and non-equilibrium situations of sub-process CO2-temperature calculations do not meet the condition. One calculates with the current concentration(14) and does not pay attention to the time it would take for the temperature of the housing shell to adjust to that value. The process time for establishing an equilibrium situation for the CO2 concentration is 53.5 years. (Excess concentration halves in 37 years.). How long would it take, for example, for the ocean in the housing shell to reach its CO2 equilibrium temperature of 420 ppM? In non-equilibrium situations, thermodynamic calculations are invalid(15).



    7. Conclusion CO2-temperature

    Our knowledge of complex systems does not justify valid statements based on the influence of the atmospheric CO2 actor on the temperature of the residential shell. Neither the required conditions for the temperature nor those for the temperature change over human scale periods are met. That is why very strict mathematical calculations lead to crazy results.



    8. Discussion and Engineers

    Engineers and many others who make statements about systems do so about complex systems, based on a single actor. How wrong that can be, even with a small inaccuracy in actor knowledge, we saw in the planet example. Engineers know this and have a cunning approach to it. They first calculate with precise physical knowledge what their system will do. Then they build it and see what it does in practice. If that doesn't work, they change it a little and look again, just until they have modified it so that it will probably work just fine for the time required.
    I give an example. A lever is needed in a machine. We know exactly which forces are appropriate for a certain length to keep the thing in balance or to make it move. If the machine doesn't do what it should do, we oil the bearings, or make the lever more robust to prevent deflection, or we change the length ratio. Just as long until the system works. It often deviates significantly from the initial design afterwards. Sometimes, however, it turns out that the system cannot do what it should. And some garbling(16) doesn't help either. For example, in ships with paddle-wheel propulsion. Changes to the wheels and engine didn't help for faster ships and in rough seas. Finally, the system went overboard and we switched to a new one, with propellers or turbines. Only practical tests learn whether the first principle approach is useful

    With garbling(16) climatologists try to adapt the 'first principle' approach of the CO2 temperature system to the observations. We can see in figure 2 that they were not successful. Complexity conditions, however, render the whole approach hopeless. Therefore, as far as the temperature of the residential shell is concerned, there is no other option than to see whether anything can be concluded with a reasonable probability from patterns of the system observations. This has been the case for centuries with engineers, doctors, and other professionals.
    The KNMI also deduces the dependence of the temperature on CO2 from patterns of measured temperature and CO2 concentration series. So practical data. The institute judged the correlation to be so strong that it made quantitative predictions. However, the method of statistical analysis used by the Institute was found to be unsound as early as 1924 on the basis of mathematical statistics. It would just as rightly designate the SP500 index as the cause of the temperature increase. But a temperature dependent on the price at which people trade stocks is not credible. Relying on practical patterns is therefore strongly dependent on the mathematical-statistical skills of the researchers(17)..

    If we do it for the temperature in our residential shell, then we should provisionally calculate based on simple trend analyzes with a temperature increase of ~1 °C/century. For sea level rise ~2 mm/year. And so on.
    Other phenomena such as the frequency and strength of hurricanes, heat waves, floods, volcanic eruptions, etc. are no indicators at all. Statements about them belong in the sphere of fortune tellers and prophets.



    9.Thanks

    Thanks to Dr. A. Huijser, Prof. Dr. C.A. de Lange, Prof. Dr. W.J. Keller, Prof. Dr. E. v.d. Heuvel for comments, improvements, corrections and encouragements

    C. (Kees) le Pair
    Nieuwegein, NL. 2022 06 12.

    10. Notes

    1. The swimming pool in my hometown, for example, is called "Sports and Event Complex".
    2. The IPCC and The Netherlands governmental Climate Intitute KNMI appeared to be aware of the complexity restrictions, although they camouflaged it effectively:
      KNMI:
      "The variability of the system poses limitations to the predictability of the climate state. Internal variations of the climate system beyond monthly time scales apart from the contribution from the positive multidecadal surface temperature trend that is currently eminent (Oldenborgh et al. 2012) and oceanic variability (Hazeleger et al. 2013), are difficult to predict and at time scales of 30 - 100 years useful predictions are basically impossible. Not only because of the large contribution of the natural variability, also because the external forcing related to human activity is considered to be unpredictable. Any attempt to make climate predictions at a relatively small spatial scale such as the Netherlands or even Western Europe for multiple decades ahead cannot be expected to lead to skilful results. KNMI
      IPCC:
      "Scenarios are images of the future, or alternative futures. They are neither predictions nor forecasts. Rather, each scenario is one alternative image of how the future might unfold. A set of scenarios assists in the understanding of possible future developments of complex systems. Some systems, those that are well understood and for which complete information is available, can be modeled with some certainty, as is frequently the case in the physical sciences, and their future states predicted. However, many physical and social systems are poorly understood, and information on the relevant variables is so incomplete that they can be appreciated only through intuition and are best communicated by images and stories. Prediction is not possible in such cases". (IPCC, 2007)
    3. E. v.d. Heuvel ,priv.com."... II have my skepticism about those climate model calculations. In my field of astrophysics we make model calculations of stars. We have four coupled differential equations as a basis, and we know the boundary conditions reasonably well (pressure and temperature at the outer edge of the star are close to zero (the temperature is not quite, but compared to the center it is), and at the center the mass and luminosity are zero, so we have four known boundary conditions). we need a whole lot of physics: nuclear reactions, transport of energy by convection or transport by absorption and re-emission, absorption coefficients at all kinds of temperatures and pressures and chemical compositions (many of them calculated in Los Alamos for atomic bombs), etc., etc,. Over fifty years of research in this area, we now have fairly good (numerically calculated) star models for stars of all kinds of masses, but we are still a long way from understanding everything, for example the strong mass loss (due to stellar winds) that you see happening with massive stars of great luminosity. And models for cool stars (red giants) in which many molecules occur in the outer layers are still very problematic, as are for red dwarfs. This star modeling problem is much simpler than that of the climate models. In addition, you have many more differential equations and many of the boundary conditions are not nearly as clear as with the star models: many of the boundary conditions (eg ocean temperature as a function of latitude, amount of snow surface, etc.) are variable. I'm not an expert on this, but my feeling is that those models must be considerably more uncertain than our star models, which are actually relatively simple, and yet still present us with problems..."
      (ClP: Prof. Van den Heuvel thinks that CO2 is an important factor in temperature increase. The CO2 concentration is clearly higher than in previous interglacials. The temperature is not different, but it still rises, about 1 °C/century Not 4 °C in 80 years, which is what the IPCC claims.)
    4. The temperature in the interior of the earth rises to 6000 °C. At the surface at high latitudes it can be -50 °C and at 15 km altitude also with +10 °C in between.
    5. Assuming that we can ascribe a temperature of 3 K (-270 °C) to the surrounding space.
    6. Data and calculation of mean radiative equilibrium temperatures as a function of reflection and emissivity: § 4, Bol, website.
    7. The Moon and the Earth may have a similar radiative environment, but they are incomparable to each other. Albedo and emissivity differ. The moon lacks ocean and atmosphere and its rotational speed is 28 times slower. The maximum temperature is 400 K (+127 °C) and the lowest measured temperature is 25 K (-248 °C). It makes no sense to draw conclusions from this for the average radiative equilibrium temperature of the earth. Moon temperatrure
    8. 180 ppM (0.018%) 20,000 years ago was dangerously low, because plants grow little or not at all at 150 ppM. Much life, including ours, is no longer possible under that.
    9. Global Carbon Project.
    10. For example, A. Huijser and I compared the CO2 stock in the air, which has been measured daily on Mauna Loa since 1960, with the CO2 that was put into the air by humans from fossil fuels. It turned out that in the period 1960 - 2020 nature gradually reversed a growing part of that increase. We found that during that period, at an atmospheric concentration of 287 ppM, naturewould have added about the same amount of CO2 annually as it takes out. We were also able to explain older measurements than those on Mauna Loa, assuming such an equilibrium in the period 1880 - 1960 of 280 ppM. The 7 ppM difference is fairly consistent with the reduced solubility in seawater at slightly higher temperatures; or the Vostok ice core measurements. We were also able to derive a process speed. The excess concentration above the current equilibrium would halve in 37 years without further human addition. We expect that an equilibrium concentration of 295 ppM can be expected in the period 2020 - 2080.
      With 420 ppM presently, the excess is currently 125 ppM. 'How does CO2 escape'? 'How does CO2 escape'?
    11. If more CO2 increases the temperature, CO2 dissolves less well in the ocean, so that the CO2 concentration in the air increases, or slows down the discharge of the excess. More CO2 makes the earth greener, which means that reflection and absorption change. More CO2 in the higher air layers increases the radiation to the universe, which increases the energy dissipation. A different temperature means a different amount of water vapor, a different and even more influential infrared absorber, H2O, has other energy transport properties. etc. the list is long.
    12. W.J. Witteman.
    13. The black dots were added later by me from the satellite measurements.
    14. For example, atmospheric CO2 is often treated using Henry's law. However, it only applies to equilibrium. There isn't. There is a continuous flow of energy and matter with intermediate process change (From solution to bacteria, plant or rock and back). There are always gradients. Those who delve into this must fall back on Onsager's cross-relationships and on hydro- and gas dynamics, not on Henry.
    15. In GCM models one even works with very fine time resolution and iteration for the CO2, but with this the whole system is not in equilibrium with regard to temperature. Condition d) is therefore not met. (Feynman's "very thoughtful mathematical calculations".)
    16. Garbling can yield very useful results, but practical results must show that. It has created many structures, systems, products, etc. and saved patients' lives. It's not necessarily negative; it just means it wasn't due to 'ab initio' calculations. However, nothing can be achieved with garbling if the goal is not attainable for valid reasons. Whoever wants to make a rocket faster than light can do whatever he wants, it won't work. It is the same with temperature predictions due to CO2.
    17. Appendix 2 (after Appendix 3) of (CLINTEL-KNMI); uncovered by mathematical statistician Prof. Dr. W.J. Keller et al. in the context of scientific advice from CLINTEL to the KNMI. The institute has persisted in its erroneous analysis for several years due to "lack of time".